Curiosities about prime numbers.Texto en inglés y traducido al español.
Interesting facts
about “Prime Numbers “
We all know the prime numbers are infinite. The Greek
mathematician Euclides proved it 23 centuries ago. Except for both prime
numbers 2 and 5, while the rest of prime numbers end in 1, 3, 7 and 9.
What is the largest
known prime number?
It was discovered that the prime numbers have the form :
2p-1 where p is a prime number.
Although not all the
numbers with this form are considered to be prime numbers.
To date, the biggest
prime numbers known is 257885161-1 which is called Mersenne
Prime. There are 174 digits
in this number which was discovered in the U.S.A.
at the University
of Missouri by Dr. C.
Cooper in 2013, within the collaborative GIMPS project, that has been searching
for the greatest prime number since 1996,
the whole proyect has been supported by a software installed on their computers
by the collaborators team.
What is the
separation gap between two prime numbers?
Except for both
numbers 2 and 3, the minimum separation
gap between 2 prime numbers is at least 2 units, and when
the separation gap is exactly 2 units, the two prime numbers are called “Twin primes “. For instance, 3 and 5
are twin numbers and so are 7 and 11.
Although it is believed
that the number of twin primes is
infinite, at present this problem is
still unsolved.
Books about prime numbers
There are countless
texts related to prime numbers. For instance, recently, a novel which employs
prime numbers was published, the book title is “ The loneliness of prime
numbers” by Paolo Giordano.
Another title of a
book with the same subject is “ El tío Petros y la conjetura de Goldbach “
by Apostolos Doxiadis.
The practical
applications or real-world
applications of prime numbers
The prime numbers are
wildly used in our daily lives, and they are most commonly used in the field of
Criptography to ensure the safety and the protection of data.
Prime numbers are used
for encrypting and decrypting messages, for example the encryption of websites
where monetary transactions are needed to be carried out in such as e-commerce
( on line shopping) or banking on line.
The internet banking (
online banking ) uses prime numbers in order to protect its consumers
information whenever a product is purchased on the internet. The banks take the
necessary precautions when they send their customers’ secret number ( Pin
number).
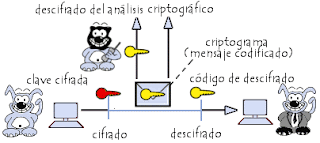
Public key
encryption . The RSA System.
In the 1970s saw the
creation of the RSA system. Let’s see how the RSA system works in practice
in a summarized form.
The users of this system have two keys to employ. One
is “the public key “ ( two numbers
represented by the letters n and
e ) as the name suggests it is not secret key; it’s accessible to all users of
the system and it can be found in a public directory. The other key is “a
private number”
( represented by the
letter d ).
We have two users of the system A and B .
supposing B sends the message M to A. M is a number.
The user B who sent
the message M looks up the user A’s
public key in the directory ( the numbers n and e ).
So by dividing M by n
we obtain the new number r
which is the remainder of the division.
In return A receives
the coded message r.
Now A needs to decode
this new message r. How is t done?
A uses its own private
key “d” ( which is only known by A ) and calculates r
to the power of d and then calculates the remainder of the
division between
The user A decrypted
the initial message which was sent by the user B and finally the user A recovers the message M.
Note: The private key
is obtained as the product of two large prime numbers.
TRANSLATION OF THE TEXT INTO SPANISH
CURIOSIDADES SOBRE NÚMEROS PRIMOS
CURIOSIDADES SOBRE NÚMEROS PRIMOS
Sabemos que el número
de números primos es infinito. El matemático griego Euclides ( 325 A.C.- 265 A.C. ) ya lo probó hace 23 siglos. Salvo
los números primos 2 y 5, el resto de números primos terminan en 1, 3, 7 ó 9.
¿Cuál es el número
primo más grande que se conoce?
Se ha descubierto que
los números primos tienen esta forma 2p -1
donde p es un número primo pero no todos los números que cumplen esa expresión
son primos.
Número de Mersenne
A día de hoy el
número primo más grande conocido es 257885161
– 1 .  Se llama número de Mersenne. este número primo tiene 17425170
dígitos. Fue descubierto en Estados Unidos en la Universidad de Missouri en Enero de 2013 por el Dr.
Curtis Cooper, dentro del proyecto colaborativo GIMPS que lleva desde 1996
buscando grandes números primos a través de un software que los colaboradores
del programa instalan en sus ordenadores.
Se llama número de Mersenne. este número primo tiene 17425170
dígitos. Fue descubierto en Estados Unidos en la Universidad de Missouri en Enero de 2013 por el Dr.
Curtis Cooper, dentro del proyecto colaborativo GIMPS que lleva desde 1996
buscando grandes números primos a través de un software que los colaboradores
del programa instalan en sus ordenadores.
¿Qué separación hay entre dos números primos?
Salvo los números
primos 2 y 3, la separación mínima entre dos números primos es al menos 2
unidades. Cuando la separación entre dos números primos es exactamente dos
unidades se llaman primos gemelos. Por ejemplo: 3 y 5 son primos gemelos, también
son primos gemelos 7 y 11.
Aunque no se ha
podido probar , se cree que existe una cantidad infinita de primos gemelos.
Existen infinidad de
de textos relacionados con los números primos, incluso recientemente se ha
publicado una novela que emplea a los números primos gemelos. El título es “ La
soledad de los números primos “ de Paolo Giordano.
Otro ejemplo de libro
que trata sobre números primos es “El tio Petros y la conjetura de Goldbach” de
Apóstolos Doxiadis.
¿Qué aplicaciones
tienen los números primos?
Los números
primos tienen una gran utilidad en la
vida diaria. Son muy usados en el campo
de la criptografía para garantizar la seguridad y protección de los datos. Los
números primos se usan para codificar y cifrar mensajes. Por ejemplo el cifrado
en páginas de Internet donde se necesita realizar transacciones monetarias como
la página web de un banco o en el comercio electrónico. Los números primos se
usan también en la banca online que están detrás de cada compra protegida en
Internet. Los bancos toman precauciones cuando envian números secretos a sus
clientes.
EL SISTEMA R.S.A.
de clave pública
En los años 70
aparece en E.E.U.U. este sistema RSA. Este sistema de clave pública RSA se usa en la
criptografía, en las contraseñas de acceso a un ordenador, en la identificación
de personas, en las tarjetas de los cajeros,
en las compras on line o por internet, etc… para proteger estos datos.
Este sistema tiene
dos claves : una clave pública
formada por dos números representadas por las letras n y e y que es accesible a todos los usuarios del
sistema y se encuentra en una guía o directorio , y una clave privada
que es un número que representamos por
la letra d y que sólo conoce el
propio usuario.
Veamos cómo funciona
este sistema de una forma resumida
´
Un usuario del sistema
B envía un mensaje m al usuario A. El
mensaje m es un número.
El usuario B busca la
clave pública del usuario A en la guía pública n y e.
Ahora se calcula el
resto de dividir la potencia me entre n. Obtenemos como resto un
número r, que es el resto de esa división.
El usuario B envía al
usuario A el número r ( es el mensaje de inicio m encriptado o
codificado).
El usuario A recibe
el mensaje r encriptado. Ahora necesita descodificarlo. ¿Cómo descodifica el
mensaje?
El usuario A coge su
clave privada, el número d, y calcula la potencia rd y calcula el
resto resultante de dividir esa potencia rd entre el número n. Ese
resultado, ese resto es justo el número de partida m.
El usuario A ya ha descodificado el mensaje r
que recibió codificado, y recibe el mensaje inicial m que le envió el usuario B. El usuario
A por lo tanto, recupera el mensaje de
partida m.
OBSERVACIÓN
Para calcular la clave privada d que se le asigna a cada usuario del sistema , se emplea un proceso
complejo basado en la factorización del
número n en números primos muy grandes.
RESOURCES WE HAVE USED TO CREATE THIS WEBSITE
We have extracted some information from lecture notes.
An also here it is some bibliography about numerical systems and prime numbers:
" El tio Petros y la conjetura de Goldbach" by Apostolos Doxiadis.
RESOURCES WE HAVE USED TO CREATE THIS WEBSITE
We have extracted some information from lecture notes.
An also here it is some bibliography about numerical systems and prime numbers:
" El tio Petros y la conjetura de Goldbach" by Apostolos Doxiadis.




Comentarios
Publicar un comentario